Databases
Introduction
A enormous amount of crap has been written on this subject: There is really only 1 satisfactory database technology: Relational. Unfortunately companies, academics, managers and developers don't accumulate kudos, sales etc by simply agreeing with a stable body of knowledge. "Dynamic" people produce "new" solutions to problems. Object database were the coming thing in the early 1990s but never took off for good reasons. "Web" databases are a joke (whatever they are supposed to be) and the popularity of XML databases has fortunately waned with the Internet boom.
The reader is referred to the Database Debunking for comments about the current state of play in the database community. The site has some drawbacks:
- C.J.Date argues (correctly) that relational database theory is the only
database model with a sound theoretical basis. Although this is an
advantage, it is nowhere near as convincing as C.J.Date seems to think it
is. Anyone who has followed the history of science and mathematics knows
that many advances (e.g. the use of differentials) were in common practice
before a sound theoretical underpinning was developed.
- The site seems to be at least partially for the promotion of books and consultancy by C.J.Date and F.Pascal. Everyone needs to make a living, but if these gentlemen were really trying to convince the world of the correctness of their viewpoints, they would publish more material on their website rather than constantly referring to their books or prompting us to buy articles.
This site is simply are compendium of the authors thought of the subject. All information is extracted from the Internet. The author refuses to buy any more books - he is currently studying Law. Updates to the site will also be infrequent. The author is however interested to hear from others who point out DB anomalies or errors in this work.
What is a Relational Database?
No known commercial database is truly relational. However...
Relations
A set is an unordered collection of objects. e.g. {cow, horse, pig} is a set containing 3 types of farm animals. The set {cow, horse, pig} is the same as the set {pig, horse, cow}. A set cannot contain the same element twice.
A tuple is an ordered collection of objects. e.g. (book, car, pig) is a tuple containing 3 objects. It is distinct from the tuples (book, pig, car), (book, car, car) and (book, pig, pig, car).
Relational databases present data as relations. i.e. unordered sets of tuples. Relations look like unordered "tables" that have no repeating rows. E.g. the relation below contains 3 tuples, and looks like the table on the right.
{ (John,Manager,£20000), (Fred,Analyst,£23000), (Mary,Analyst,£21000) } |
|
The individual components of each tuple is called an attribute. The set of values from which attribute values are drawn is called the the attribute domain. In the example above, the domain of the first attribute consists of the set of possible employee names, the domain of the second attribute consists of the set of job titles, and the domain of the third attribute consist of the set of monetary amounts.
More precisely, a relation is a subset of the cartesian product of the attribute domains. i.e. a reation R Ì D1 x D2 x ... x Dn where Di is the ith attribute domain.
Keys
Superkey: a set of attributes that unique identify a row. In the example
above, the name uniquely identifies a row in the table. So does the name
+ job title.
Candidate key: a superkey for which no proper subset is a superkey. In the
example below, name + job title is not a candidate key since name
alone can be used to identify rows.
Primary key: a chosen candidate key.
Foreign Key: a set of attributes that matches exactly the primary key of
another table.
Dependencies / Relationships
Notation: (name ® salary) means the attribute salary is functionally dependent on the attribute name. (The enclosing bracket are optional) A functional dependency (name ® salary) exists if 2 observers that agree on the value of a name attribute, then they must necessarily agree on the value of the corresponding salary attribute. More formally, if a relation R contains the tuples (x,y) and (x,y'), and (x ® y), then y=y'.
(job ®* salary) means that there is a one to many relationship from attribute job and salary. (The enclosing bracket are optional) A one to many relationship exists from job to salary if knowledge of the value of a job variable selects the range of possible values for the salary attribute.
(job *«* salary) means that there is a many to many relationship between attribute salary and job. (The enclosing bracket are optional) More formally, if (x *®* y), then there exists a relation R with attributes x and y. Also (x ® y) implies (x *«* y), and (x ®* y) implies (x *«* y).
Relational Operators
New relations can be constructing applying the following set operations to existing relations.
- Union (È).
- Intersection (Ç).
- Difference (-).
- Projection (p).
- Selection (s).
- Natural Join (
 ).
). - Cartesian Product (x).
- Division (/).
Notes: (1) "Renaming" (r) a query is
sometimes included in this list, but is not a mathematical operation.
(2) Natural
joins can be implemented as a selection and projection on the cartesian product
of relations. E.g. the Employees and Jobs tables are shown below.
|
|
Job is the primary key of Jobs table, and a foreign key in the Employees table. The natural join is constructed by (1) generating the cartesian product of the 2 tables ( Employee x Job ), shown below,
| Name | Employees.Job | Jobs.Job | Salary |
| John | Manager | Manager | £30,000 |
| John | Manager | Analyst | £22,000 |
| Fred | Analyst | Manager | £30,000 |
| Fred | Analyst | Analyst | £22,000 |
| Mary | Analyst | Manager | £30,000 |
| Mary | Analyst | Analyst | £22,000 |
(2) restricting the relation to rows where the Job columns are equal, shown below, and
| Name | Employees.Job | Jobs.Job | Salary |
| John | Manager | Manager | £30,000 |
| Fred | Analyst | Analyst | £22,000 |
| Mary | Analyst | Analyst | £22,000 |
(3) creating a projection showing only one Job column.
| Name | Job | Salary |
| John | Manager | £30,000 |
| Fred | Analyst | £22,000 |
| Mary | Analyst | £22,000 |
Algebraically (for those who like such things), Employee ![]() Jobs = p(Name, Jobs.Job,Salary) (s(Employees.Job=Jobs.Job)(Employees
x Jobs))
Jobs = p(Name, Jobs.Job,Salary) (s(Employees.Job=Jobs.Job)(Employees
x Jobs))
Nulls
The use of Nulls in SQL causes significant problems. E.g. in the table below, does NULL indicate that Mary does not receive a salary (works on an hourly rate), or that the value is unknown?
| Name | Job | Salary |
| John | Manager | £30,000 |
| Fred | Manager | £32,000 |
| Mary | Analyst | NULL |
If Mary does not receive a salary, then it is questionable that an "entry" should exist for her salary in any table. One method is to put the table in 6NF. See below.
The problem associated with Nulls is made worse by the inconsistent treatment on Nulls by various database vendors.
Normal Forms
Normalisation is based on the observation that certain relations (normal forms) have the same information content as other relations but have "nice" properties with respect to operations such as inserts, updates and deletes. Normal forms are organised into a hierarchy. 1NF => 2 NF => 3NF => 4NF => 5NF.
1st Normal Form
Description
The 1NF requires that data is presented as a relation. I.e. it is presented as a table, and the data in each column is atomic.
Example
Structure A (not 1NF)
| Job | Name |
| Manager | John |
| Analyst | Fred, Mary |
Structures B,C (1NF)
|
|
|||||||||||||||
|
Structure B |
Structure C |
Structure A is put in 1NF by creating separate entries for each name (structure B), or by defining the domain of Name to consist of possible sets of names (structure C).
2nd Normal Form
Description
A relation is in 2NF if every non-key attribute is fully dependent on each candidate key of the relation. I.e. If the table has a composite candidate key, candidate_key, and dependency (candidate_key ® c), then there does not exist a dependency (a ® c) where a is part of, but not the whole candidate key.
2NF is the first step towards saying that a relation is "about" the dependency generator (key).
Example
Structure A
| Title | Publisher | Publisher Address | Author | Number Sold | Price |
| Database Fundamentals | Thick Books Ltd | 1 High St | J. Smith | 23 | £30.95 |
| C++ Programming | Complex Books Ltd | 2 Olive Grove | T. Jones | 450 | £40.99 |
| Database Fundamentals | White Books Ltd | 3 Low Road | D. White | 65 | £42.99 |
The table above shows books sold. (Assume) a book title is only unique to a publisher. I.e. the primary key is Title, Publisher. The following dependencies exist:
(Title, Publisher ®
Price)
(Title, Publisher ®
Author)
(Title, Publisher ®
Number Sold)
(Publisher ® Publisher Address)
Structure B (2NF)
|
|
The first table is "about" the book and the second table is
"about" the publisher.
The first table incorporates the following dependencies
(Title, Publisher ®
Price)
(Title, Publisher ®
Author)
(Title, Publisher ®
Number Sold)
The second table incorporates the following dependencies
(Publisher -> Publisher Address)
Update Anomolies
| Name | Job | Salary |
| John | Manager | 30,000 |
| Fred | Analyst | 22,000 |
| Mary | Analyst | 22,000 |
The table above is in 2NF since (Name ® Job) and (Name ® Salary). However (Job ® Salary) so updating a Salary requires updates to multiple rows.
3rd Normal Form
Description
A relation is in 3NF if it is in 2NF and every non-key attribute is non-transitively dependent on each candidate key. I.e. there does not exists any attributes a, b, c such that
- a is a candidate key,
- there exists dependencies (a ® b) and (b ® c)
Like to say that relations in 3NF are "about" the dependency generator (primary key). Still question: Is there only 1 primary key?
Example 1:
Structure A
| Name | Job | Salary |
| John | Manager | 30,000 |
| Fred | Analyst | 22,000 |
| Mary | Analyst | 22,000 |
Name is the primary key, and there are transitive dependencies (Name ® Job) and (Job ® Salary). It is therefore not in 3NF.
Structure B (3NF)
|
|
Structure A can be put in 3NF by splitting it into 2 tables, one for each dependency generator Name and Job.
Example 2:
Structure A
| Order# | Quantity | Unit Price | Total |
| 123 | 100 | £23.50 | £2,350 |
| 124 | 40 | £12.50 | £500 |
The attribute Total in structure A depends on
Structure B (3NF)
| Order# | Quantity | Unit Price |
| 123 | 100 | £23.50 |
| 124 | 40 | £12.50 |
Boyce-Codd Normal Form
A relation is in BCNF if it is in 3NF and
4th Normal Form
5th Normal Form
6th Normal Form
Description
6NF is not widely accepted at this time. A table is in 6NF if and only if the relation consists of at most the primary key and another attribute, and there are no null values in the table.
Example
Structure A
| Name | Job | Telephone | Salary |
| John | Manager | 020 7281 1234 | 20,000 |
| Fred | Analyst | 020 7281 1234 | 22,000 |
| Mary | Analyst | NULL | 23,000 |
Structure B (6NF)
|
|
|
Advantages
6NF model single functional dependencies. It provides a mechanism for (1) removing nulls from the database, (2) providing the equivalence of table and views.
Codd's 12 Rules
Codd's famous rules outline what are supposed to be the characteristics of a relational database. For a time, these rules where used as a checklist to determine how well database vendors conformed to the relational model. Comment: Not all these rules are logical consequences of the requirement that a database management system be based on set theory and predicate calculus.
Rule 1: The Information Rule
Data should be presented to users as relations (sets of ntuples). I.e.
Data should be presented to users as tables with no defined row or column order.
See previous definition of Relational Database.
Comment: ![]() Current
implementations fall short even in regard to this rule - SQL allows the creation
of unnamed columns (E.g. SELECT a, b, a+b FROM TABLE table_name). As a
consequence, these columns must be accessed by column number.
Current
implementations fall short even in regard to this rule - SQL allows the creation
of unnamed columns (E.g. SELECT a, b, a+b FROM TABLE table_name). As a
consequence, these columns must be accessed by column number.
Rule 2: Guaranteed Access
Any "atom" of data must be accessible without ambiguity by specifying the table name, key and column name.
Rule 3: Systematic Treatment of Null Values
A field should be allowed to remain empty. This involves the support of a null value, which is distinct from an empty string or a number with a value of zero. Of course, this can't apply to primary keys. Most database implementations support the concept of a non-null fields.
Comment: ![]() NULLs create all sorts of anomalies. The treatment of NULLs divides the relational world.
There are two main approaches:
NULLs create all sorts of anomalies. The treatment of NULLs divides the relational world.
There are two main approaches:
- Reject the use of NULLs altogether. (6NF)
- Use 4 valued logic: true, false, null and unknown. (Codd)
Both approaches are equivalent (isomorphic), however the author believes that the 6NF is more fundamental. More about this later.
Rule 4: Dynamic On-Line Catalog Based on the Relational Model
Meta-data is data. A relational database must provide access to it's meta-data through the same mechanism used to access "normal" data. This is accomplished by storing the structure information in "system" tables.
Rule 5: Comprehensive Database Language
The database must support a language that provides data definition, data manipulation, data integrity, and
database transaction control.
Comment: ![]() All commercial "relational" databases use
some form of SQL as their supported comprehensive
language. SQL is deficient in many regards.
All commercial "relational" databases use
some form of SQL as their supported comprehensive
language. SQL is deficient in many regards.
It seem ridiculous to the author that a single language is expected to satisfy all the requirements specified above. In particular, the specification of real world constraints can be arbitrarily complex and requires the full power of languages such as C++ and Java..
Rule 6: Views are Updatable
Data can be presented to the user in different logical combinations, called views. Each view should support the same full range of data manipulation that direct-access to a table has available. In practice, providing update and delete access to logical views is difficult and is not fully supported by any current database.
Comment: ![]()
Rule 7: High-level Insert, Update, and Delete
Data can be retrieved from a relational database in sets constructed of data from multiple rows and/or multiple tables. This rule states that insert, update, and delete operations should be supported for any retrievable set rather than just for a single row in a single table.
Comment: ![]() SQL
INSERT, UPDATE and DELETE statements sux (see below). Multi-row and multi-table
operations are impleneted in SQL using transactions.
SQL
INSERT, UPDATE and DELETE statements sux (see below). Multi-row and multi-table
operations are impleneted in SQL using transactions.
Rule 8: Physical Data Independence
The user is isolated from the physical method of storing and retrieving information from the database. Changes can be made to the underlying architecture (hardware, disk storage methods) without affecting how the user accesses it.
Comment: ![]() In practise,
RDBMS systems often require "hints" such as the explicit definition of
indices to achieve acceptable performance. This is a failing of current RDBMS
implementations rather the Relational model. The problem of optimising queries however
is hard and influenced by the database language. More about this later.
In practise,
RDBMS systems often require "hints" such as the explicit definition of
indices to achieve acceptable performance. This is a failing of current RDBMS
implementations rather the Relational model. The problem of optimising queries however
is hard and influenced by the database language. More about this later.
Rule 9: Logical Data Independence
Views should not change when the logical (table) structure of the database changes.
Comment: ![]() Current
implementations require each view to be manually revised after changes are made
to underlying tables. The difficulties associated with implementing this rule
can be seen in the example below.
Current
implementations require each view to be manually revised after changes are made
to underlying tables. The difficulties associated with implementing this rule
can be seen in the example below.
Structure A:
| Name | Job | Salary |
| John | Manager | 20,000 |
| Fred | Analyst | 22,000 |
| Mary | Analyst | 23,000 |
Structure B:
|
|
Going A -> B, maintain A as view: The dependency (Name ® Salary) is replaced by dependencies (Name ® Job, Job ® Salary). The new dependency cannot be created until Salary values are updated so that a dependency (Job->Salary) exist.
Shorcoming of SQL- typical steps: (1) Create new table for Job, Salary, (2) Update Salary information so dependency (Job->Salary) exists, (3) Copy Salary information from original table to Job Salary table, (4) Drop Salary from original table, (5) Create view to "replace" original table. If the change is to atomic, then changes must be made within a transaction. At no time are dependency relationships explicit.
Going B -> A, maintain B as view: The dependency (Job ® Salary) is not longer valid, the dependency (Name->Job) already exists via transtitive dependency (Name ® Job, Job ® Salary) = (Name ® Salary) and is retained.
Rule 10: Integrity Independence
The database language should support constraints that maintain database integrity.
Comment: ![]() This rule is not
implemented. See rule 5. SQL databases (generally) implement the following:
This rule is not
implemented. See rule 5. SQL databases (generally) implement the following:
- No component of a primary key can have a null value. (see rule 3)
- If a foreign key is defined in one table, any value in it must exist as a primary key in another table.
How should database constraints be made available to client applications?
Rule 11: Distribution Independence
Users should not be aware of whether or not the database is distributed.
Rule 12: No Subversion
There should be no way to modify the database structure other than through the database language.
Comment: Most databases today support
administrative tools (typically GUIs) that do allow "direct manipulation" of the
database structure, however the essence of this requirement is that these tools
should always be implementable as applications that only use the database
language to interface with the database.
Current "Relational" implementations
- View and "base" tables should have the same status. This is pure Codd. Unfortunately Universities teach "ANSI-SPARC" crap - views are built on top of tables. ANSI-Sparc is a flawed implementation common amongst current "rational" databases, not a principle!
- Problem with NULLs. Most important is that presence of NULL stops views from being updatable. Also confusion with meaning - does NULL mean "missing (unknown)" or "not defined". More about this later.
- The SQL INSERT statement sux - should be able to insert data in any way consistent with constraints. Doesn't matter about physical storage - no need to (should not!) be tables. Again, flawed relational implementations.
- SQL specific shortcomings - lots of these.
- N-tier => constraints implemented in "business objects" duplicates constraints etc in database. Constraints (some) implemented again in presentation layer. Database needs suitable call level interface to provide this type of information to clients.
The Third Manifesto (C.J.Date & H.Darwen)
- rejects NULLs completely. D&H define 6NF just to get rid of all NULLs. Also 6NF provides mechanism for implementing equivalence of views and tables. (6NF is primitive)
- rejects the standard mapping (objects => tables).
- restricts objects to domain values (column data types). OO is regarded as being orthogonal to Relational DB.
- The domain type system is based on "principle of substitution" - inheritance by restriction.
- rejects SQL.
- Propose a new language, D, to replace SQL.
Object-Relational Mapping
Intuitively objects are just aggregates of attributes and methods => type system with (multiple) inheritance, but introduces NULLs. Since the issue of NULLs is at the heart of how Object-relational mappings should be done, the issue of NULLs needs to be explored in detail.
- Objects don't need to be in any "normal" form.
- "Standard" object-relational mapping: Tuples in T looks like (<a1,v1>, <a2,v2>, ...,<an, vn>). Tuples in T ' are derived from T if they look like (<a1,v1>, <a2,v2>, ...,<an, vn>,..., <am, vm>). Basic problem: T ' has different dimension from T. Maybe principle of substitution needs some rewording. E.g. Principle of Substitution: T' is derived from T if there exists a project operator P such that P.t' can subsitute for an element of T where t' is an element of T'. (Removes the need for NULLs)
- NULLs needed to "pad" out values in "derived" tables. Codd suggested 4 value logic system. true, false, missing, null.
Can both approaches are correct? Common 3NF can reconstructed from 6NF, and visa versa.
Object Fragility
There is a tendency amongst new developers to believe that objects somehow “model the real world” and have an objective existence. This image is reinforced by the relative hegemony of Java and Microsoft libraries - many new programmers only ever use one String class, one set of windowing classes, one set of Database classes, etc. In reality objects are fragile and tied closely to a particular problem space. Java and .NET object hierarchies work only because they force users to think in a particular way. If there is no pre-existing dominant object model, different developers working on the similar problems will almost certainly develop very different solutions.
Object fragility is also responsible for another well-known phenomena: the wrapper classes. Corporations are forever attempting to promote code reuse and produce common shared libraries, however the author’s experience indicates that such libraries and their object models typically have very short half-lives (perhaps only 6 months). Why? The usual suspects - new users have slightly different requirements, the business environment changes, previous incorrect assumptions are exposed, the scope of the library is expanded etc. The result is libraries (which still needs to be supported) that are continually wrapped by newer (better?) versions (The author has seen packages containing 6+ wrapper layers), and is always a bug ridden tangled mess that no-one fully understands. The functionality that a developer typically wants is in layers 3 and 4 of 6 where he can’t get at it.
Object models are fragile, so the ability to navigate between objects using operations is also fragile. I.e. Object networks show the same fragility noted in network databases over 20 years ago.
Fragility is acceptable in application object networks: changes to an application object model only affect the application. Changes to an object database model however impacts all database users and applications. I.e. Application object fragility is generally considered acceptable but object database fragility is not.
R - a Relational Programming Language
Many years ago the author embarked on a large C++ COM project. Anyone who has done this knows exactly how tricky this type of thing is: complex object networks, changes to the design results in significant reworking of code introducing reference counting bugs that were nightmares to find…etc
The solution adopted was to build containers for each object type and query the container to get the appropriate objects. Objects no longer held references to each other; rather they stored the names or ID (foreign keys) of any objects they might wish to access in the future. The result was a spectacular success: Reference counting bugs almost vanished and the application proved extremely resilient to changes.
The diagram below shows what the author and many others believe in the relationship between tables and objects. Objects are viewed as less fundamental than relations. It is quite possible to believe that a simple A.I. process could identify attributes and dependencies in many situations. (TODO: expand). Tables (views) are then built up from attributes and dependencies, as specified elsewhere in this document. In contrast, OOA identifies objects, attributes and operations from the analysis of natural language descriptions. Nouns => objects, attributes. Verbs => operations. I.e. OOA requires a natural language analysis capability, and a natural language description that is sufficiently rich that it contains a complete object model! Furthermore, many relational processes such as normalisation are implicitly (subconsciously) applied during OOA.
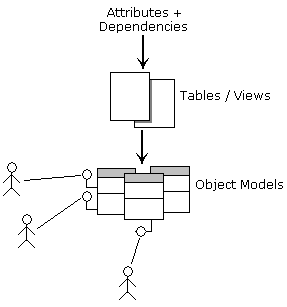
Attributes and dependencies are stored in 6NF. Tables (views) are built on top of the stored attributes and dependencies, and are viewed as derived entities. Objects map directly to tables.
Fundamental Differences between objects and tuples
Tables represent sets. No two rows in the table can have exactly the same values. Object "identity" essential.
Applications contain many objects that have the same value but are distinct - variables are references to unique objects. Distinction between updating an object (attribute updated), and updating a variable (object reference updated)
What is special about OO?
(1) Concentration on behaviours -
"Contracts" established between objects.
(2) Polymorphism. Why are object hierarchies so useful? No idea. Very puzzling.
Need to think about this.
R - specification
The following is a proposed simple programming language that use relational database concepts to manage application objects.
R regards attributes, functional dependencies and relationship as fundamental. Tables (views) and objects are derived objects, and often tied to a specific application. R therefore divides statements in 4 parts:
- attribute, functional dependency and relationship definitions.
- attribute, functional dependency and relationship create/update/delete statements.
- table (view) and object definitions.
- standard programming language constructs such as if-then-else, loops and assignments.
There is no garbage collection - objects are persistent.
Proposed grammar: (Currently bollocks - this needs lots of work)
body = (dependency_declaration | alter_statement | type_declaration | statement) [ body ]; |
Attribute, Functional Dependency and Relationship Definitions
Proposed grammar:
dependency_declaration = attribute_declaration | dependency;
attribute_declaration = "attribute" attribute type_declaration ";" ;
dependency = attribute [ "(" type_declaration ")" ] dependency_type attribute [ where_clause ] ";" ;
dependency_type = ("->" | "->*" | "*<->*")
|
Attribute, Functional Dependency and Relationship Update/Delete Statements
Proposed grammar:
alter_statement = delete_statement | replace_statement delete_statement = "delete" dependency_declaration; // xxxx - bollocks, blah, blah replace_statement = "replace" dependency_declaration "with" dependency_declaration [ "," dependency_declaration ]; |
Table (view) and Object Definitions
No distinction is made between rowset and object. ?? Should implement concept of interface...
Proposed grammar:
type_declaration = "class" type_name "(" determinant ")" [ extends_clause ] "{" [ dependent_attributes ] operations "}";
extends_clause = "is" type_name where_clause;
|
Programming Language Constructs
Proposed grammar:
rowset_declaration = "rowset" "<" type_name ">" variable_name "=" type_name "(" criteria ")" ";";
variable_declaration = type_name variable_name [ "=" expr ] ";";
statement = assignment | conditional | loop | "{" statement "}";
assignment = variable_name "=" expr;
expr = ... | NULL | UNKNOWN;
conditional = "if" "(" boolean_expr ")" statement [ "else" statement ];
loop = "for" "(" statement ";" boolean_expr ";" statement ")" statement ;
|
Example 1
The following code section declares an Employee class and enumerates the employees currently stored in the database.
...
System system = System().first();
...
// Dependencies - these effectively define a "table" with primary key name.
name (string) -> job (string);
name -> address (string);
name -> post_code (string);
name -> salary (decimal);
// Class declaration
class Employee ( name ) // Do we need to include name? Is this a hangover from SQL thinking?
{
job;
address;
post_code;
salary;
}
// Rowset declaration
Rowset<Employee> employees = Employee (post_code='N7 9SH');
// Statement (loop)
for(Employee employee = employees.first();
employee != null;
employee = employees.next())
{
system.println("employee name is " + employee.name + "\n");
}
Example 2
The following code section (1) extends the Employee class by adding a job description, and (2) enumerates the employees currently stored in the database.
// New dependency
job -> description (string);
class Employee2 ( name ) is Employee
{
job_description;
}
// Rowset declaration
Rowset<Employee2> employees = Employee2 (post_code='N7 9SH');
// Statement (loop)
for(Employee2 employee = employees.first();
employee != null;
employee = employees.next())
{
system.println("employee name is " + employee.name + ", job description is " + employee.job_description + "\n");
}
Example 3
The following is based on an London Metropolitan University assignment.
Each employee in a company has a title, name, address, telephone number, e-mail address and national insurance number. The company runs a number of research projects, and employs researchers to work on the projects. A researcher may work on more than one project, and project typically involves more than one researcher. Each researcher is a specialist is some research area. The company develops software packages for clients. Each developer is familar with a number of development tools. Company consultants provide support for the various applications developed by the company. Each consultant may support more than one application, and each application may be supported by more than one consultant. Only company manager can edit details stored by the company.
This leads to the UML class diagram shown below.
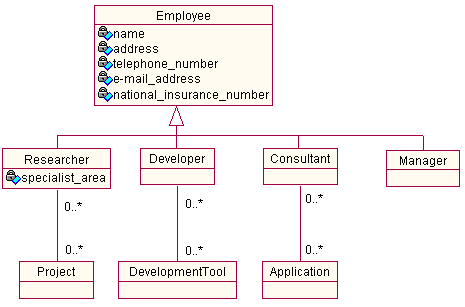
But what happens if a researcher is also a developer? or a developer is promoted to manager? The object model above cannot cope.
// Dependencies
NI_number(string) -> name(string);
NI_number -> address(string);
NI_number -> telephone_number(string);
NI_number -> e-mail_address(string);
NI_number -> address(string);
NI_number -> employee_type(string);
NI_number -> specialist_area(string) WHERE employee_type(NI_number)='Researcher';
NI_number ->* development_tool(string) WHERE employee_type(NI_number)='Developer'
NI_number ->* application(string) WHERE employee_type(NI_number)='Consultant'
// Class declarations
class Employee ( NI_number )
{
name; address; telephone_number; e-mail_address; employee_type;
}
class Researcher ( NI_number ) is Employee WHERE employee_type(NI_number)='Researcher'
{
specialist_area;
project;
}
class Developer ( NI_number ) is Employee WHERE employee_type(NI_number)='Developer'
{
development_tool;
}
// Rowset declaration
Rowset<Employee> employees = Employee();
// Statement (loop)
for(Employee2 employee = employees.first();
employee != null;
employee = employees.next())
{
system.println("employee name is " + employee.name + "\n");
}
What happens if a researcher is also a developer? The dependency NI_number -> employee_type(string); simply becomes NI_number ->* employee_type(string);
Classes and code using them remains usable!
Example 4
Account Statement
// Dependencies
txn_id(numeric) -> txn_date(datetime);
txn_id -> description(string);
posting_id(numeric) -> amount(numeric));
posting_id -> account(string);
account,txn_id -> balance(numeric);
// Not at all sure the best way to do this.
txn_id ->* posting_id;
posting_id -> txn_id;
class ReportRow (txn_id, posting_id, account)
WHERE posting_id(txn_id) = posting_id(posting_id)
AND txn_id(account,txn_id) = txn_id(txn_id) // <= this sux. maybe? Needs some work.
{
txn_id; txn_date; description; account; amount; balance;
}
// Rowset declaration
Rowset<ReportRow> rows = ReportRow();
// Statement (loop)
for(ReportRow row = rows.first();
row != null;
row = rows.next())
{
system.println(row.txn_id + "\t"
+ row.txn_date + "\t"
+ row.description + "\t"
+ row.balance + "\t"
+ row.amount);
}
Example 5
Properties
// Dependencies
id(numeric) -> provider_name(string);
id -> description(string);
id -> version(numeric));
class Component_1 (id) {provider_name;}
class Component_2 (id) {description;}
class Component_3 (id) {version;}
class Component_12 (id) {provider_name;description;}
class Component_23 (id) {description;version;}
class Component_13 (id) {provider_name;version;}
class Component_123 (id) {provider_name;description;version;}
Last Updated. 3-March-2003